Why Meta Stability Can Be Removed With Two Flip Flops

Electronic circuit with two stable states

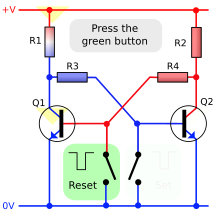
An animated interactive SR latch (R1, R2 = 1kΩ; R3, R4 = 10kΩ).

In electronics, a flip-flop or latch is a excursion that has two stable states and can be used to store state information – a bistable multivibrator. The excursion tin can be fabricated to change state by signals applied to ane or more command inputs and will take one or two outputs. It is the basic storage element in sequential logic. Flip-flops and latches are fundamental building blocks of digital electronics systems used in computers, communications, and many other types of systems.

Flip-flops and latches are used as data storage elements. A flip-flop is a device which stores a unmarried bit (binary digit) of data; one of its two states represents a "ane" and the other represents a "nil". Such information storage can exist used for storage of state, and such a circuit is described equally sequential logic in electronics. When used in a finite-land machine, the output and next state depend non only on its current input, but likewise on its current state (and hence, previous inputs). It tin likewise be used for counting of pulses, and for synchronizing variably-timed input signals to some reference timing bespeak.

Flip-flops tin can be either level-triggered (asynchronous, transparent or opaque) or edge-triggered (synchronous, or clocked). The term flip-bomb has historically referred generically to both level-triggered and border-triggered circuits that store a single bit of information using gates. Recently, some authors reserve the term flip-bomb exclusively for discussing clocked circuits; the uncomplicated ones are commonly called transparent latches.^{[1] [2]} Using this terminology, a level-sensitive flip-flop is called a transparent latch, whereas an edge-triggered flip-flop is simply called a flip-flop. Using either terminology, the term "flip-flop" refers to a device that stores a single bit of data, only the term "latch" may besides refer to a device that stores whatever number of bits of data using a unmarried trigger. The terms "border-triggered", and "level-triggered" may be used to avoid ambivalence.^[3]

When a level-triggered latch is enabled it becomes transparent, but an edge-triggered flip-bomb'southward output simply changes on a single type (positive going or negative going) of clock edge.

History [edit]

Flip-flop schematics from the Eccles and Jordan patent filed 1918, i fatigued equally a cascade of amplifiers with a positive feedback path, and the other as a symmetric cross-coupled pair

The starting time electronic flip-flop was invented in 1918 by the British physicists William Eccles and F. W. Jordan.^{[4] [five]} It was initially called the Eccles–Jordan trigger circuit and consisted of two agile elements (vacuum tubes).^[6] The design was used in the 1943 British Colossus codebreaking computer^[vii] and such circuits and their transistorized versions were common in computers even after the introduction of integrated circuits, though flip-flops made from logic gates are also mutual at present.^{[eight] [nine]} Early flip-flops were known variously as trigger circuits or multivibrators.

According to P. Fifty. Lindley, an engineer at the Us Jet Propulsion Laboratory, the flip-flop types detailed below (SR, D, T, JK) were first discussed in a 1954 UCLA course on computer design past Montgomery Phister, so appeared in his book Logical Design of Digital Computers. ^{[10] [11]} Lindley was at the time working at Hughes Aircraft under Eldred Nelson, who had coined the term JK for a flip-bomb which inverse states when both inputs were on (a logical "i"). The other names were coined by Phister. They differ slightly from some of the definitions given below. Lindley explains that he heard the story of the JK flip-flop from Eldred Nelson, who is responsible for coining the term while working at Hughes Shipping. Flip-flops in utilize at Hughes at the time were all of the type that came to be known equally J-1000. In designing a logical system, Nelson assigned messages to flip-flop inputs as follows: #1: A & B, #2: C & D, #3: E & F, #4: G & H, #v: J & Grand. Nelson used the notations "j-input" and "k-input" in a patent awarding filed in 1953.^[12]

Implementation [edit]

Flip-flops tin can be either simple (transparent or asynchronous) or clocked (synchronous). In the context of hardware description languages, the elementary ones are commonly described as latches,^[one] while the clocked ones are described equally flip-flops.^[2]

Simple flip-flops can be congenital around a unmarried pair of cross-coupled inverting elements: vacuum tubes, bipolar transistors, field effect transistors, inverters, and inverting logic gates accept all been used in practical circuits.

Clocked devices are peculiarly designed for synchronous systems; such devices ignore their inputs except at the transition of a defended clock betoken (known as clocking, pulsing, or strobing). Clocking causes the flip-flop either to change or to retain its output indicate based upon the values of the input signals at the transition. Some flip-flops change output on the ascension edge of the clock, others on the falling edge.

Since the elementary amplifying stages are inverting, two stages can be connected in succession (as a cascade) to course the needed non-inverting amplifier. In this configuration, each amplifier may be considered every bit an active inverting feedback network for the other inverting amplifier. Thus the two stages are connected in a non-inverting loop although the circuit diagram is usually drawn as a symmetric cantankerous-coupled pair (both the drawings are initially introduced in the Eccles–Jordan patent).

Flip-bomb types [edit]

Flip-flops tin can be divided into common types: the SR ("set-reset"), D ("data" or "delay"^[xiii]), T ("toggle"), and JK. The behavior of a item type can be described by what is termed the feature equation, which derives the "next" (i.e., afterward the side by side clock pulse) output, Q _next in terms of the input signal(south) and/or the electric current output, ${\displaystyle Q}$ .

Unproblematic set-reset latches [edit]

When using static gates as building blocks, the most fundamental latch is the simple SR latch, where South and R stand for set and reset. It can exist constructed from a pair of cantankerous-coupled NOR or NAND logic gates. The stored bit is present on the output marked Q.

SR NOR latch [edit]

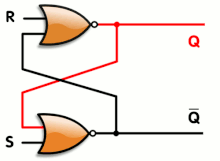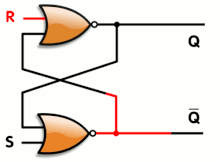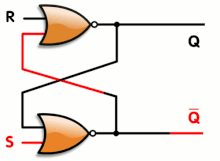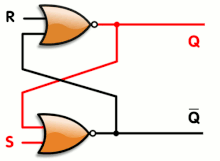
An blitheness of a SR latch, constructed from a pair of cantankerous-coupled NOR gates. Red and black mean logical '1' and '0', respectively.

An animated SR latch. Blackness and white hateful logical '1' and '0', respectively.

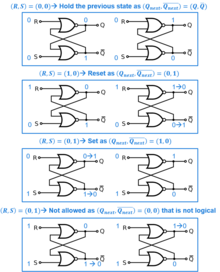
1. Due south = i, R = 0: Gear up
2. S = 0, R = 0: Hold
3. Due south = 0, R = ane: Reset
4. S = 1, R = 1: Non immune

Transitioning from the restricted combination (D) to (A) leads to an unstable state.

While the R and S inputs are both low, feedback maintains the Q and Q outputs in a constant state, with Q the complement of Q. If S (Set) is pulsed loftier while R (Reset) is held low, so the Q output is forced high, and stays high when S returns to low; similarly, if R is pulsed high while Due south is held low, then the Q output is forced low, and stays low when R returns to low.

SR latch operation^[3]

Characteristic table				Excitation table
S	R	Qnext	Action	Q	Qnext	South	R
0	0	Q	Hold state	0	0	0	X
0	ane	0	Reset	0	i	ane	0
ane	0	1	Set	one	0	0	1
1	1	X	Non allowed	1	1	X	0

Note: X ways don't care, that is, either 0 or 1 is a valid value.

The R = S = 1 combination is called a restricted combination or a forbidden state because, equally both NOR gates then output zeros, information technology breaks the logical equation Q = not Q. The combination is also inappropriate in circuits where both inputs may go low simultaneously (i.east. a transition from restricted to keep). The output would lock at either 1 or 0 depending on the propagation time relations betwixt the gates (a race status).

How an SR NOR latch works.

To overcome the restricted combination, one tin add gates to the inputs that would convert (Due south, R) = (1, 1) to one of the non-restricted combinations. That can be:

• Q = ane (1, 0) – referred to as an South (dominated)-latch
• Q = 0 (0, 1) – referred to as an R (dominated)-latch

This is done in well-nigh every programmable logic controller.

• Keep state (0, 0) – referred to as an Due east-latch

Alternatively, the restricted combination tin be made to toggle the output. The issue is the JK latch.

The characteristic equation for the SR latch is :

${\displaystyle Q_{\text{next}}={\bar {R}}Q+{\bar {R}}Southward}$ or ${\displaystyle Q_{\text{next}}={\bar {R}}(Q+S).}$ ^[14]

Another expression is :

${\displaystyle Q_{\text{next}}=S+{\bar {R}}Q}$ with ${\displaystyle SR=0}$ ^[15]

SR NAND latch [edit]

An SR latch constructed from cross-coupled NAND gates.

The circuit shown below is a bones NAND latch. The inputs are generally designated S and R for Gear up and Reset respectively. Because the NAND inputs must normally be logic i to avoid affecting the latching action, the inputs are considered to be inverted in this circuit (or agile low).

The excursion uses feedback to "call back" and retain its logical state even after the decision-making input signals have changed. When the S and R inputs are both loftier, feedback maintains the Q outputs to the previous state.

SR latch operation S R Activeness 0 0 Q = 1, Q = 1; not allowed 0 one Q = 1 1 0 Q = 0 1 1 No modify; random initial

Symbol for an SR NAND latch

SR AND-OR latch [edit]

An SR AND-OR latch. Light green means logical 'one' and dark greenish means logical '0'. The latch is currently in hold fashion (no change).

From a instruction point of view, SR latches drawn as a pair of cross-coupled components (transistors, gates, tubes, etc.) are often hard to understand for beginners. A didactically easier to empathise way is to depict the latch as a single feedback loop instead of the cross-coupling. The following is an SR latch built with an AND gate with i inverted input and an OR gate. Annotation that the inverter is non needed for the latch functionality, just rather to make both inputs High-agile.

SR AND-OR latch performance

S	R	Activity
0	0	No modify; random initial
i	0	Q = 1
Ten	1	Q = 0

Note that the SR AND-OR latch has the benefit that Due south = ane, R = 1 is well defined. In to a higher place version of the SR AND-OR latch it gives priority to the R bespeak over the Due south indicate. If priority of S over R is needed, this can be accomplished by connecting output Q to the output of the OR gate instead of the output of the AND gate.

The SR AND-OR latch is easier to understand, because both gates can be explained in isolation. When neither S or R is set up, and then both the OR gate and the AND gate are in "hold mode", i.e., their output is the input from the feedback loop. When input South = one, then the output of the OR gate becomes ane, regardless of the other input from the feedback loop ("set style"). When input R = i then the output of the AND gate becomes 0, regardless of the other input from the feedback loop ("reset fashion"). And since the output Q is directly connected to the output of the AND gate, R has priority over South. Latches fatigued equally cross-coupled gates may wait less intuitive, as the behaviour of one gate appears to be intertwined with the other gate.

Note that the SR AND-OR latch tin exist transformed into the SR NOR latch using logic transformations: inverting the output of the OR gate and also the 2nd input of the AND gate and connecting the inverted Q output between these ii added inverters; with the AND gate with both inputs inverted existence equivalent to a NOR gate according to De Morgan's laws.

JK latch [edit]

The JK latch is much less often used than the JK flip-flop. The JK latch follows the following country table:

JK latch truth tabular array

J	Yard	Qadjacent	Comment
0	0	Q	No change
0	1	0	Reset
1	0	ane	Ready
1	1	Q	Toggle

Hence, the JK latch is an SR latch that is made to toggle its output (oscillate between 0 and 1) when passed the input combination of 11.^[xvi] Unlike the JK flip-flop, the eleven input combination for the JK latch is not very useful considering there is no clock that directs toggling.^[17]

Gated latches and conditional transparency [edit]

Latches are designed to be transparent. That is, input point changes cause immediate changes in output. Additional logic tin can be added to a unproblematic transparent latch to make information technology non-transparent or opaque when some other input (an "enable" input) is not asserted. When several transparent latches follow each other, using the same enable signal, signals tin propagate through all of them at once. However, by following a transparent-high latch with a transparent-depression (or opaque-high) latch, a principal–slave flip-bomb is implemented.

Gated SR latch [edit]

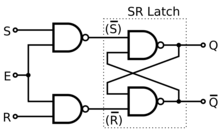
NAND Gated SR Latch (Clocked SR flip-flop). Annotation the inverted inputs.

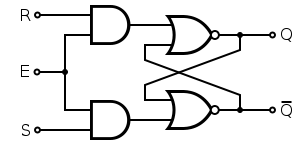
A gated SR latch circuit diagram constructed from AND gates (on left) and NOR gates (on correct).

A synchronous SR latch (sometimes clocked SR flip-flop) can be made by adding a second level of NAND gates to the inverted SR latch (or a second level of AND gates to the direct SR latch). The extra NAND gates farther invert the inputs so SR latch becomes a gated SR latch (and a SR latch would transform into a gated SR latch with inverted enable).

With East high (enable true), the signals can pass through the input gates to the encapsulated latch; all signal combinations except for (0, 0) = concur then immediately reproduce on the (Q, Q) output, i.due east. the latch is transparent.

With E low (enable false) the latch is closed (opaque) and remains in the land it was left the last time East was high.

The enable input is sometimes a clock signal, but more ofttimes a read or write strobe. When the enable input is a clock betoken, the latch is said to be level-sensitive (to the level of the clock signal), as opposed to border-sensitive like flip-flops below.

Gated SR latch operation E/C Action 0 No activeness (continue country) 1 The same as non-clocked SR latch

Symbol for a gated SR latch

Gated D latch [edit]

This latch exploits the fact that, in the 2 active input combinations (01 and 10) of a gated SR latch, R is the complement of Due south. The input NAND stage converts the ii D input states (0 and 1) to these ii input combinations for the adjacent SR latch by inverting the data input signal. The low state of the enable indicate produces the inactive "11" combination. Thus a gated D-latch may be considered every bit a one-input synchronous SR latch. This configuration prevents application of the restricted input combination. It is too known as transparent latch, data latch, or merely gated latch. It has a data input and an enable signal (sometimes named clock, or control). The word transparent comes from the fact that, when the enable input is on, the indicate propagates straight through the circuit, from the input D to the output Q. Gated D-latches are besides level-sensitive with respect to the level of the clock or enable signal.

Transparent latches are typically used equally I/O ports or in asynchronous systems, or in synchronous ii-stage systems (synchronous systems that use a two-stage clock), where two latches operating on different clock phases forbid data transparency as in a master–slave flip-flop.

Latches are available as integrated circuits, usually with multiple latches per chip. For example, 74HC75 is a quadruple transparent latch in the 7400 serial.

The truth tabular array below shows that when the enable/clock input is 0, the D input has no effect on the output. When E/C is high, the output equals D.

Gated D latch truth table Due east/C D Q Q Comment 0 10 Qprev Q prev No change 1 0 0 ane Reset 1 1 i 0 Prepare

Symbol for a gated D latch

• 

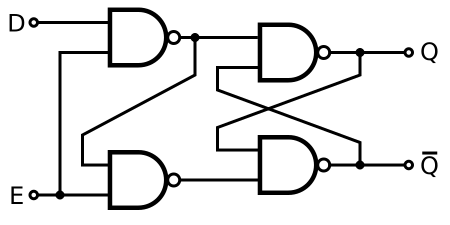
  A gated D latch based on an SR NAND latch

• 

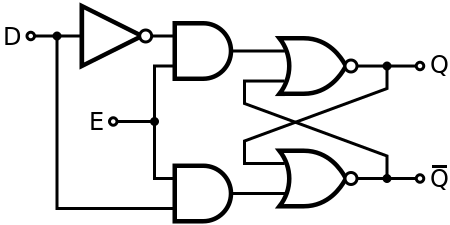
  A gated D latch based on an SR NOR latch

• 

  An blithe gated D latch. Black and white hateful logical 'one' and '0', respectively.

  1. D = 1, E = one: prepare
  2. D = 1, Due east = 0: hold
  3. D = 0, E = 0: hold
  4. D = 0, E = ane: reset

• 

  A gated D latch in pass transistor logic, similar to the ones in the CD4042 or the CD74HC75 integrated circuits.

Earle latch [edit]

The classic gated latch designs have some undesirable characteristics.^[18] They require double-track logic or an inverter. The input-to-output propagation may have upwards to three gate delays. The input-to-output propagation is not abiding – some outputs accept two gate delays while others take three.

Designers looked for alternatives.^[nineteen] A successful alternative is the Earle latch. It requires merely a single data input, and its output takes a constant 2 gate delays. In addition, the two gate levels of the Earle latch can, in some cases, be merged with the last two gate levels of the circuits driving the latch because many mutual computational circuits have an OR layer followed by an AND layer as their last two levels. Merging the latch function tin implement the latch with no additional gate delays.^[18] The merge is ordinarily exploited in the design of pipelined computers, and, in fact, was originally developed by John G. Earle to be used in the IBM Arrangement/360 Model 91 for that purpose.^[20]

The Earle latch is take chances free.^[21] If the heart NAND gate is omitted, so one gets the polarity concur latch, which is ordinarily used because it demands less logic.^{[21] [22]} Nonetheless, it is susceptible to logic gamble. Intentionally skewing the clock bespeak can avoid the gamble.^[22]

• 

  Earle latch uses complementary enable inputs: enable active low (E_L) and enable active high (E_H)

• 

  An animated Earle latch. Blackness and white mean logical 'ane' and '0', respectively.

  1. D = 1, E_H = 1: set
  2. D = 0, E_H = 1: reset
  3. D = ane, E_H = 0: hold

D flip-flop [edit]

D flip-flop symbol

The D flip-flop is widely used. Information technology is also known as a "information" or "filibuster" flip-flop.

The D flip-flop captures the value of the D-input at a definite portion of the clock cycle (such equally the rising edge of the clock). That captured value becomes the Q output. At other times, the output Q does not change.^{[23] [24]} The D flip-flop can be viewed as a memory cell, a zero-guild concur, or a delay line.^[25]

Truth tabular array:

Clock	D	Qnext
Ascent edge	0	0
Ascent edge	1	1
Non-ascension	Ten	Q

(Ten denotes a don't intendance condition, meaning the signal is irrelevant)

Most D-type flip-flops in ICs have the adequacy to be forced to the set or reset land (which ignores the D and clock inputs), much like an SR flip-flop. Usually, the illegal S = R = 1 condition is resolved in D-type flip-flops. Setting S = R = 0 makes the flip-flop behave every bit described above. Hither is the truth table for the other possible S and R configurations:

Inputs				Outputs
S	R	D	>	Q	Q
0	1	X	X	0	1
1	0	Ten	X	1	0
i	1	10	Ten	1	1

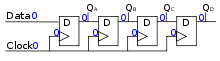
These flip-flops are very useful, as they grade the basis for shift registers, which are an essential role of many electronic devices. The advantage of the D flip-bomb over the D-type "transparent latch" is that the signal on the D input pivot is captured the moment the flip-flop is clocked, and subsequent changes on the D input will exist ignored until the next clock event. An exception is that some flip-flops accept a "reset" signal input, which volition reset Q (to zilch), and may exist either asynchronous or synchronous with the clock.

The above circuit shifts the contents of the register to the right, 1 bit position on each active transition of the clock. The input X is shifted into the leftmost scrap position.

Classical positive-edge-triggered D flip-flop [edit]

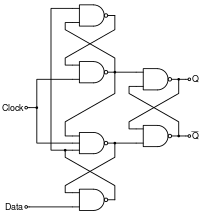
A positive-edge-triggered D flip-flop

A positive-border-triggered D flip-flop with set and reset

This excursion^[26] consists of two stages implemented by SR NAND latches. The input stage (the two latches on the left) processes the clock and information signals to ensure correct input signals for the output phase (the single latch on the right). If the clock is depression, both the output signals of the input stage are high regardless of the data input; the output latch is unaffected and it stores the previous state. When the clock point changes from low to high, only one of the output voltages (depending on the data betoken) goes low and sets/resets the output latch: if D = 0, the lower output becomes low; if D = 1, the upper output becomes low. If the clock signal continues staying loftier, the outputs keep their states regardless of the information input and strength the output latch to stay in the corresponding state as the input logical zero (of the output stage) remains active while the clock is high. Hence the role of the output latch is to store the data only while the clock is low.

The excursion is closely related to the gated D latch as both the circuits convert the 2 D input states (0 and 1) to two input combinations (01 and 10) for the output SR latch past inverting the data input signal (both the circuits separate the unmarried D bespeak in two complementary South and R signals). The difference is that in the gated D latch unproblematic NAND logical gates are used while in the positive-border-triggered D flip-flop SR NAND latches are used for this purpose. The role of these latches is to "lock" the agile output producing low voltage (a logical zero); thus the positive-edge-triggered D flip-flop can also exist idea of every bit a gated D latch with latched input gates.

Master–slave edge-triggered D flip-flop [edit]

A primary–slave D flip-flop. Information technology responds on the falling edge of the enable input (unremarkably a clock)

An implementation of a main–slave D flip-bomb that is triggered on the rising edge of the clock

A master–slave D flip-bomb is created by connecting 2 gated D latches in series, and inverting the enable input to one of them. Information technology is chosen master–slave because the master latch controls the slave latch'due south output value Q and forces the slave latch to hold its value whenever the slave latch is enabled, every bit the slave latch always copies its new value from the principal latch and changes its value just in response to a alter in the value of the master latch and clock signal.

For a positive-edge triggered master–slave D flip-flop, when the clock bespeak is low (logical 0) the "enable" seen by the first or "master" D latch (the inverted clock signal) is loftier (logical 1). This allows the "master" latch to store the input value when the clock signal transitions from low to loftier. Equally the clock signal goes high (0 to one) the inverted "enable" of the first latch goes low (1 to 0) and the value seen at the input to the master latch is "locked". Nearly simultaneously, the twice inverted "enable" of the second or "slave" D latch transitions from low to high (0 to one) with the clock signal. This allows the indicate captured at the rising edge of the clock past the now "locked" master latch to pass through the "slave" latch. When the clock signal returns to low (1 to 0), the output of the "slave" latch is "locked", and the value seen at the last rising edge of the clock is held while the "principal" latch begins to have new values in preparation for the next ascension clock edge.

Removing the leftmost inverter in the circuit creates a D-type flip-flop that strobes on the falling border of a clock signal. This has a truth table like this:

D	Q	>	Qnext
0	X	Falling	0
1	X	Falling	1

Dual-edge-triggered D flip-flop [edit]

An implementation of a dual-edge-triggered D flip-bomb

Flip-Flops that read in a new value on the ascent and the falling edge of the clock are called dual-border-triggered flip-flops. Such a flip-bomb may exist built using two unmarried-border-triggered D-type flip-flops and a multiplexer as shown in the paradigm.

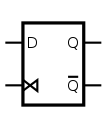
Excursion symbol of a dual-edge-triggered D flip-flop

Edge-triggered dynamic D storage element [edit]

A CMOS IC implementation of a dynamic edge-triggered flip-flop with reset

An efficient functional alternative to a D flip-flop tin be fabricated with dynamic circuits (where information is stored in a capacitance) as long every bit information technology is clocked often plenty; while not a true flip-flop, it is yet called a flip-flop for its functional role. While the master–slave D chemical element is triggered on the border of a clock, its components are each triggered by clock levels. The "border-triggered D flip-flop", as it is chosen even though it is non a truthful flip-flop, does not take the main–slave backdrop.

Edge-triggered D flip-flops are often implemented in integrated high-speed operations using dynamic logic. This means that the digital output is stored on parasitic device capacitance while the device is non transitioning. This design of dynamic flip flops also enables simple resetting since the reset operation tin exist performed past simply discharging one or more internal nodes. A common dynamic flip-flop variety is the true single-phase clock (TSPC) blazon which performs the flip-bomb performance with piddling power and at high speeds. Withal, dynamic flip-flops will typically non work at static or depression clock speeds: given enough time, leakage paths may belch the parasitic capacitance enough to crusade the flip-flop to enter invalid states.

T flip-flop [edit]

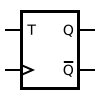
A circuit symbol for a T-blazon flip-flop

If the T input is high, the T flip-flop changes country ("toggles")^[27] whenever the clock input is strobed. If the T input is low, the flip-flop holds the previous value. This behavior is described by the feature equation:

${\displaystyle Q_{\text{next}}=T\oplus Q=T{\overline {Q}}+{\overline {T}}Q}$ (expanding the XOR operator)

and can exist described in a truth table:

T flip-flop performance^[28]

Characteristic table				Excitation table
${\displaystyle T}$	${\displaystyle Q}$	${\displaystyle Q_{\text{next}}}$	Annotate	${\displaystyle Q}$	${\displaystyle Q_{\text{next}}}$	${\displaystyle T}$	Comment
0	0	0	Hold country (no clock)	0	0	0	No change
0	1	i	Concur state (no clock)	ane	1	0	No change
1	0	1	Toggle	0	ane	ane	Complement
1	ane	0	Toggle	1	0	i	Complement

When T is held high, the toggle flip-flop divides the clock frequency by ii; that is, if clock frequency is four MHz, the output frequency obtained from the flip-flop will be 2 MHz. This "split up by" feature has application in various types of digital counters. A T flip-flop tin also exist built using a JK flip-bomb (J & K pins are continued together and deed equally T) or a D flip-flop (T input XOR Q_previous drives the D input).

JK flip-flop [edit]

A circuit symbol for a positive-edge-triggered JK flip-flop

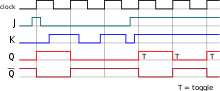
JK flip-flop timing diagram

The JK flip-flop augments the beliefs of the SR flip-flop (J: Set, Grand: Reset) by interpreting the J = K = ane condition every bit a "flip" or toggle command. Specifically, the combination J = i, K = 0 is a command to set the flip-flop; the combination J = 0, Thou = ane is a control to reset the flip-flop; and the combination J = Chiliad = 1 is a command to toggle the flip-flop, i.e., modify its output to the logical complement of its current value. Setting J = K = 0 maintains the current state. To synthesize a D flip-flop, simply set Yard equal to the complement of J (input J will human action as input D). Similarly, to synthesize a T flip-bomb, prepare 1000 equal to J. The JK flip-flop is therefore a universal flip-flop, considering information technology tin can be configured to work as an SR flip-bomb, a D flip-flop, or a T flip-bomb.

The characteristic equation of the JK flip-bomb is:

${\displaystyle Q_{\text{next}}=J{\overline {Q}}+{\overline {K}}Q}$

and the corresponding truth table is:

JK flip-bomb operation^[28]

Feature table				Excitation table
J	M	Annotate	Qadjacent	Q	Qadjacent	Annotate	J	K
0	0	Concur state	Q	0	0	No change	0	X
0	one	Reset	0	0	one	Set	1	X
one	0	Set	i	1	0	Reset	Ten	ane
1	1	Toggle	Q	one	1	No alter	Ten	0

Timing considerations [edit]

Timing parameters [edit]

Flip-flop setup, hold and clock-to-output timing parameters

The input must be held steady in a menstruum around the rising edge of the clock known as the aperture. Imagine taking a picture of a frog on a lily-pad.^[29] Suppose the frog then jumps into the water. If you take a picture of the frog every bit information technology jumps into the h2o, you will become a blurry motion picture of the frog jumping into the water—it's not clear which country the frog was in. But if yous take a moving picture while the frog sits steadily on the pad (or is steadily in the h2o), you will get a clear picture. In the same way, the input to a flip-flop must be held steady during the aperture of the flip-flop.

Setup fourth dimension is the minimum corporeality of time the data input should be held steady before the clock event, and so that the data is reliably sampled by the clock.

Hold fourth dimension is the minimum amount of fourth dimension the data input should be held steady after the clock consequence, and then that the information is reliably sampled by the clock.

Aperture is the sum of setup and concord time. The data input should be held steady throughout this time period.^[29]

Recovery fourth dimension is the minimum amount of fourth dimension the asynchronous set or reset input should be inactive earlier the clock effect, so that the data is reliably sampled by the clock. The recovery time for the asynchronous set or reset input is thereby like to the setup fourth dimension for the information input.

Removal time is the minimum amount of time the asynchronous set or reset input should be inactive afterward the clock upshot, and then that the data is reliably sampled by the clock. The removal time for the asynchronous set up or reset input is thereby like to the concord time for the data input.

Short impulses practical to asynchronous inputs (fix, reset) should not be applied completely inside the recovery-removal period, or else it becomes entirely indeterminable whether the flip-bomb volition transition to the advisable state. In another case, where an asynchronous signal merely makes 1 transition that happens to fall between the recovery/removal time, somewhen the flip-bomb volition transition to the advisable state, just a very brusque glitch may or may not appear on the output, dependent on the synchronous input signal. This 2nd situation may or may not have significance to a excursion design.

Set and Reset (and other) signals may be either synchronous or asynchronous and therefore may exist characterized with either Setup/Concord or Recovery/Removal times, and synchronicity is very dependent on the design of the flip-flop.

Differentiation betwixt Setup/Concur and Recovery/Removal times is ofttimes necessary when verifying the timing of larger circuits considering asynchronous signals may be found to be less disquisitional than synchronous signals. The differentiation offers circuit designers the ability to ascertain the verification conditions for these types of signals independently.

Metastability [edit]

Flip-flops are subject to a problem called metastability, which tin can happen when two inputs, such as data and clock or clock and reset, are changing at about the same time. When the order is not clear, inside appropriate timing constraints, the consequence is that the output may behave unpredictably, taking many times longer than normal to settle to one state or the other, or even aquiver several times before settling. Theoretically, the fourth dimension to settle downward is non bounded. In a computer organization, this metastability tin cause corruption of data or a programme crash if the state is non stable earlier another circuit uses its value; in particular, if two different logical paths utilize the output of a flip-flop, one path can interpret it as a 0 and the other as a one when it has not resolved to stable state, putting the auto into an inconsistent state.^[30]

The metastability in flip-flops can exist avoided by ensuring that the information and command inputs are held valid and abiding for specified periods earlier and after the clock pulse, called the setup time (t_su) and the concur time (t_h) respectively. These times are specified in the data canvas for the device, and are typically between a few nanoseconds and a few hundred picoseconds for mod devices. Depending upon the flip-flop's internal organization, information technology is possible to build a device with a naught (or even negative) setup or hold time requirement merely not both simultaneously.

Unfortunately, it is not always possible to meet the setup and hold criteria, considering the flip-bomb may be connected to a real-time signal that could alter at any time, exterior the control of the designer. In this case, the best the designer can do is to reduce the probability of mistake to a certain level, depending on the required reliability of the circuit. Ane technique for suppressing metastability is to connect two or more flip-flops in a concatenation, so that the output of each one feeds the data input of the adjacent, and all devices share a common clock. With this method, the probability of a metastable event can be reduced to a negligible value, but never to zero. The probability of metastability gets closer and closer to zero every bit the number of flip-flops connected in series is increased. The number of flip-flops being cascaded is referred to as the "ranking"; "dual-ranked" flip flops (two flip-flops in serial) is a common state of affairs.

Then-called metastable-hardened flip-flops are bachelor, which work by reducing the setup and hold times equally much as possible, but even these cannot eliminate the trouble entirely. This is because metastability is more than than simply a matter of circuit design. When the transitions in the clock and the data are close together in time, the flip-flop is forced to decide which event happened first. However fast the device is fabricated, there is e'er the possibility that the input events will be so shut together that information technology cannot detect which one happened first. It is therefore logically impossible to build a perfectly metastable-proof flip-flop. Flip-flops are sometimes characterized for a maximum settling time (the maximum time they will remain metastable under specified conditions). In this case, dual-ranked flip-flops that are clocked slower than the maximum allowed metastability fourth dimension volition provide proper conditioning for asynchronous (e.m., external) signals.

Propagation delay [edit]

Some other important timing value for a flip-flop is the clock-to-output delay (mutual symbol in data sheets: t_CO) or propagation filibuster (t_P), which is the time a flip-flop takes to change its output after the clock edge. The time for a loftier-to-low transition (t_PHL) is sometimes dissimilar from the time for a depression-to-high transition (t_PLH).

When cascading flip-flops which share the aforementioned clock (equally in a shift annals), it is of import to ensure that the t_CO of a preceding flip-flop is longer than the concur fourth dimension (t_h) of the following flip-flop, so data nowadays at the input of the succeeding flip-flop is properly "shifted in" following the active edge of the clock. This human relationship between t_CO and t_h is ordinarily guaranteed if the flip-flops are physically identical. Furthermore, for correct operation, it is easy to verify that the clock flow has to exist greater than the sum t_su + t_h.

Generalizations [edit]

Flip-flops can be generalized in at least two ways: past making them 1-of-N instead of 1-of-2, and past adapting them to logic with more than two states. In the special cases of 1-of-3 encoding, or multi-valued ternary logic, such an element may exist referred to as a flip-flap-bomb.^[31]

In a conventional flip-bomb, exactly one of the ii complementary outputs is high. This can be generalized to a retentivity element with N outputs, exactly one of which is loftier (alternatively, where exactly one of N is low). The output is therefore ever a one-hot (respectively ane-common cold) representation. The structure is like to a conventional cross-coupled flip-flop; each output, when loftier, inhibits all the other outputs.^[32] Alternatively, more or less conventional flip-flops tin exist used, one per output, with additional circuitry to make sure just ane at a time can be true.^[33]

Some other generalization of the conventional flip-bomb is a memory element for multi-valued logic. In this instance the retentivity chemical element retains exactly one of the logic states until the command inputs induce a change.^[34] In addition, a multiple-valued clock can also be used, leading to new possible clock transitions.^[35]

See also [edit]

Wikimedia Eatables has media related to Flip-flops.

• Latching relay
• Positive feedback
• Pulse transition detector
• Static random-access retention
• Sample and concord, analog latch

References [edit]

1. ^ ^{a b} Pedroni, Volnei A. (2008). Digital electronics and design with VHDL. Morgan Kaufmann. p. 329. ISBN978-0-12-374270-iv.
2. ^ ^{a b} Latches and Flip Flops (EE 42/100 Lecture 24 from Berkeley) "...Sometimes the terms flip-bomb and latch are used interchangeably..."
3. ^ ^{a b} Roth, Charles H. Jr. "Latches and Flip-Flops." Fundamentals of Logic Design. Boston: PWS, 1995. Impress.
4. ^ William Henry Eccles and Frank Wilfred Jordan, "Improvements in ionic relays" British patent number: GB 148582 (filed: 21 June 1918; published: five August 1920).
5. ^ Run across:
   • W. H. Eccles and F. West. Jordan (19 September 1919) "A trigger relay utilizing iii-electrode thermionic vacuum tubes," The Electrician, 83 : 298.
   • Reprinted in: West. H. Eccles and F. W. Jordan (December 1919) "A trigger relay utilizing three-electrode thermionic vacuum tubes," The Radio Review, 1 (3) : 143–146.
   • Summary in: W. H. Eccles and F. Westward. Jordan (1919) "A trigger relay utilising 3 electrode thermionic vacuum tubes," Written report of the Eighty-seventh Meeting of the British Clan for the Advancement of Scientific discipline: Bournemouth: 1919, September 9–13, pp. 271–272.
6. ^ Pugh, Emerson Due west.; Johnson, Lyle R.; Palmer, John H. (1991). IBM'southward 360 and early 370 systems . MIT Press. p. 10. ISBN978-0-262-16123-seven.
7. ^ Flowers, Thomas H. (1983), "The Pattern of Colossus", Annals of the History of Computing, 5 (3): 249, doi:ten.1109/MAHC.1983.10079, S2CID 39816473
8. ^ Gates, Earl D. (2000-12-01). Introduction to electronics (4th ed.). Delmar Thomson (Cengage) Learning. p. 299. ISBN978-0-7668-1698-5.
9. ^ Fogiel, Max; Gu, Y'all-Liang (1998). The Electronics problem solver, Book 1 (revised ed.). Research & Education Assoc. p. 1223. ISBN978-0-87891-543-9.
10. ^ P. Fifty. Lindley, Aug. 1968, EDN (magazine), (letter dated June 13, 1968).
11. ^ Phister, Montgomery (1958). Logical Design of Digital Computers. Wiley. p. 128. ISBN9780608102658.
12. ^ United states of america 2850566, Eldred C. Nelson, "High-Speed Printing System", published Sept. viii, 1953, issued Sept. 2, 1958 ; page 15
13. ^ Shiva, Sajjan G. (2000). Calculator pattern and architecture (3rd ed.). CRC Press. p. 81. ISBN978-0-8247-0368-4.
14. ^ Langholz, Gideon; Kandel, Abraham; Mott, Joe Fifty. (1998). Foundations of Digital Logic Design. Singapore: Earth Scientific Publishing Co. Ptc. Ltd. p. 344. ISBN978-981-02-3110-1.
15. ^ "Summary of the Types of Flip-flop Behaviour". Retrieved on 16 April 2018.
16. ^ Hinrichsen, Diederich; Pritchard, Anthony J. (2006). Mathematical Systems Theory I: Modelling, Country Space Assay, Stability and Robustness. Springer. pp. 63–64. ISBN9783540264101.
17. ^ Farhat, Hassan A. (2004). Digital design and computer organization. Vol. 1. CRC Press. p. 274. ISBN978-0-8493-1191-8.
18. ^ ^{a b} Kogge, Peter Chiliad. (1981). The Architecture of Pipelined Computers. McGraw-Hill. pp. 25–27. ISBN0-07-035237-2.
19. ^ Cotten, L. Westward. (1965). "Circuit Implementation of High-Speed Pipeline Systems". AFIPS Proc. Autumn Joint Computer Conference: 489–504. doi:10.1145/1463891.1463945. S2CID 15955626.
20. ^ Earle, John G. (March 1965). "Latched Carry-Save Adder". IBM Technical Disclosure Message. seven (10): 909–910.
21. ^ ^{a b} Omondi, Amos R. (1999-04-thirty). The Microarchitecture of Pipelined and Superscalar Computers. Springer. pp. xl–42. ISBN978-0-7923-8463-2.
22. ^ ^{a b} Kunkel, Steven R.; Smith, James E. (May 1986). "Optimal Pipelining in Supercomputers". ACM SIGARCH Estimator Architecture News. ACM. 14 (two): 404–411 [406]. CiteSeerX10.1.i.99.2773. doi:ten.1145/17356.17403. ISSN 0163-5964. S2CID 2733845.
23. ^ The D Flip-Flop
24. ^ "Edge-Triggered Flip-flops". Archived from the original on 2013-09-08. Retrieved 2011-12-15 .
25. ^ A Survey of Digital Computer Memory Systems
26. ^ SN7474 TI datasheet
27. ^ "Understanding the T Flip-Bomb". oemsecrets.com . Retrieved 29 Apr 2021.
28. ^ ^{a b} Mano, M. Morris; Kime, Charles R. (2004). Logic and Computer Pattern Fundamentals, 3rd Edition. Upper Saddle River, NJ, United states of america: Pearson Education International. p. 283. ISBN0-13-191165-1.
29. ^ ^{a b} Harris, Southward; Harris, D (2016). Digital Design and Reckoner Architecture - ARM Edition. Morgan Kaufmann, Waltham, MA. ISBN978-0-12-800056-4.
30. ^ Chaney, Thomas J.; Molnar, Charles Eastward. (April 1973). "Anomalous Behavior of Synchronizer and Czar Circuits". IEEE Transactions on Computers. C-22 (four): 421–422. doi:10.1109/T-C.1973.223730. ISSN 0018-9340. S2CID 12594672.
31. ^ Often attributed to Don Knuth (1969) (come across Midhat J. Gazalé (2000). Number: from Ahmes to Cantor. Princeton University Printing. p. 57. ISBN978-0-691-00515-vii. ), the term flip-flap-bomb actually appeared much before in the calculating literature, for instance, Bowdon, Edward K. (1960). The design and application of a "flip-flap-flop" using tunnel diodes (Master'south thesis). University of North Dakota. , and in Alexander, W. (February 1964). "The ternary computer". Electronics and Power. IET. x (two): 36–39. doi:ten.1049/ep.1964.0037.
32. ^ "Ternary "flip-flap-flop"". Archived from the original on 2009-01-05. Retrieved 2009-ten-17 .
33. ^ United states of america 6975152
34. ^ Irving, Thurman A.; Shiva, Sajjan G.; Nagle, H. Troy (March 1976). "Flip-Flops for Multiple-Valued Logic". IEEE Transactions on Computers. C-25 (3): 237–246. doi:10.1109/TC.1976.5009250. S2CID 34323423.
35. ^ Wu, Haomin; Zhuang Nan (1991). "Inquiry into ternary edge-triggered JKL flip-flop". Journal of Electronics (People's republic of china). 8 (Book viii, Number 3 / July, 1991): 268–275. doi:10.1007/BF02778378. S2CID 61275953.

External links [edit]

• FlipFlop Hierarchy Archived 2015-04-08 at the Wayback Machine, shows interactive flipflop circuits.
• The J-K Flip-Flop

mitchelllinquis.blogspot.com

Source: https://en.wikipedia.org/wiki/Flip-flop_(electronics)

Share this post